Cálculo
- Para cálculo infinitesimal (diferencial o integral) véase Cálculo infinitesimal
- Para el estudio de los números reales, los complejos, los vectores y sus funciones véase Análisis matemático
En general el termino cálculo (del latín calculus = piedra)[1] hace referencia, indistintamente, a la acción o el resultado correspondiente a la acción de calcular. Calcular, por su parte, consiste en realizar las operaciones necesarias para prever el resultado de una acción previamente concebida, o conocer las consecuencias que se pueden derivar de unos datos previamente conocidos.
No obstante, el uso más común del término cálculo es el lógico-matemático. Desde esta perspectiva, el cálculo consiste en un procedimiento mecánico, o algoritmo, mediante el cual podemos conocer las consecuencias que se derivan de unos datos previamente conocidos.
Concepto general de cálculo
El cálculo es un sistema de símbolos no interpretados, es decir, sin significado alguno, en el que se establecen mediante reglas estrictas, las relaciones sintácticas entre los símbolos para la construcción de fórmulas bien formadas (fbf), así como las reglas que permiten transformar dichas expresiones en otras equivalentes; entendiendo por equivalentes que ambas tienen siempre y de forma necesaria el mismo valor de verdad. Dichas transformaciones son meramente tautologías.
Un cálculo consiste en:
- Un conjunto de elementos primitivos. Dichos elementos pueden establecerse por enumeración, o definidos por una propiedad tal que permita discernir sin duda alguna cuándo un elemento pertenece o no pertenece al sistema.
- Un conjunto de reglas de formación de “expresiones bien formadas”(EBFs) que permitan en todo momento establecer, sin forma de duda, cuándo una expresión pertenece al sistema y cuándo no.
- Un conjunto de reglas de transformación de expresiones, mediante las cuales partiendo de una expresión bien formada del cálculo podremos obtener una nueva expresión equivalente y bien formada que pertenece al cálculo.
Cuando en un cálculo así definido se establecen algunas expresiones determinadas como verdades primitivas o axiomas, decimos que es un sistema formal axiomático.
Un cálculo así definido si cumple al mismo tiempo estas tres condiciones decimos que es un Cálculo Perfecto:
- Es consistente: No es posible que dada una expresión bien formada del sistema, f, y su negación, no − f, sean ambas teoremas del sistema. No puede haber contradicción entre las expresiones del sistema.
- Decidible: Dada cualquier expresión bien formada del sistema podemos encontrar un método que nos permita decidir mediante una serie finita de operaciones si dicha expresión es o no es un teorema del sistema.
- Completo: Cuando dada cualquier expresión bien formada del sistema, podemos establecer la demostración o prueba de que es un teorema del sistema.
La misma lógica-matemática ha demostrado que tal sistema de cálculo perfecto "no es posible"
El cálculo lógico
Entendemos aquí por cálculo lógico, un algoritmo que permite cómoda y fácilmente inferir o deducir un enunciado verdadero a partir de otro u otros que se tienen como válidamente verdaderos.
La inferencia o deducción es una operación lógica que consiste en obtener un enunciado como conclusión a partir de otro(s) (premisas) mediante la aplicación de reglas de inferencia.[15]
Decimos que alguien infiere -o deduce- "T" de "R" si acepta que si "R" tiene valor de verdad V, entonces, necesariamente, "T" tiene valor de verdad V.
Los hombres en nuestra tarea diaria, utilizamos constantemente el razonamiento deductivo. Partimos de enunciados empíricos -supuestamente verdaderos y válidos- para concluir en otro enunciado que se deriva de aquellos, según las leyes de la lógica natural.[16]
La lógica, como ciencia formal, se ocupa de analizar y sistematizar dichas leyes, fundamentarlas y convertirlas en las reglas que permiten la transformación de unos enunciados -premisas- en otros -conclusiones- con objeto de convertir las operaciones en un algoritmo riguroso y eficaz, que garantiza que dada la verdad de las premisas, la conclusión es necesariamente verdadera.
Al aplicar las reglas de este cálculo lógico a los enunciados que forman un argumento mediante la simbolización adecuada de fórmulas o Expresiones bien formadas (EBF) construimos un modelo o sistema deductivo.
Sistematización de un cálculo de deducción natural
Reglas de formación de fórmulas
I. Una letra enunciativa (con o sin subíndice) es una EBF.
II. Si A es una EBF, ¬ A también lo es.
III. Si A es una EBF y B también, entonces A  B; A
B; A  B; A
B; A  B; A
B; A  B, también lo son.
B, también lo son.
 B; A
B; A  B; A
B; A  B; A
B; A  B, también lo son.
B, también lo son.IV. Ninguna expresión es una fórmula del Cálculo sino en virtud de I,II,III.
- Notas:
- A, B,... con mayúsculas están utilizadas como metalenguaje en el que cada variable expresa cualquier proposición, atómica (p,q,r,s....) o molecular (p/\q), (p\/q)...
- A, B,... son símbolos que significan variables; ¬,
 ,
,  , →,
, →,  , son símbolos constantes.
, son símbolos constantes. - Existen diversas formas de simbolización. Utilizamos aquí la de uso más frecuente en España.[17]
Reglas de transformación de fórmulas
1) Regla de sustitución (R.T.1):
Dada una tesis EBF del cálculo, en la que aparecen variables de enunciados, el resultado de sustituir una, algunas o todas esas variables por expresiones bien formadas (EBF) del cálculo, será también una tesis EBF del cálculo. Y ello con una única restricción, si bien muy importante: cada variable ha de ser sustituida siempre que aparece y siempre por el mismo sustituto.
Veamos el ejemplo:
| 1 | ![\left [ \left ( p \land q \right ) \lor r \right ]\rightarrow t \lor s](http://upload.wikimedia.org/math/b/4/5/b45fe9c8e29197866d3b68f0abeb4de9.png) | Transformación |
| 2 |  | donde 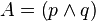 ; y donde ; y donde  |
| 3 | 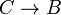 | donde  |
O viceversa
| 1 | 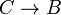 | Transformación |
| 2 |  | donde  |
| 3 | ![\left [ \left ( p \land q \right ) \lor r \right ]\rightarrow t \lor s](http://upload.wikimedia.org/math/b/4/5/b45fe9c8e29197866d3b68f0abeb4de9.png) | donde  ; y donde ; y donde  |
2) Regla de separación (R.T.2):
Si X es una tesis EBF del sistema y lo es también X  Y, entonces Y es una tesis EBF del sistema.
Y, entonces Y es una tesis EBF del sistema.
 Y, entonces Y es una tesis EBF del sistema.
Y, entonces Y es una tesis EBF del sistema.Esquemas de inferencia
Sobre la base de estas dos reglas, siempre podremos reducir un argumento cualquiera a la forma:
![[A \land B \land C....\land N]\rightarrow Y](http://upload.wikimedia.org/math/c/0/7/c070f1d0b0229e87de57b7c651e3274a.png)
lo que constituye un esquema de inferencia en el que una vez conocida la verdad de cada una de las premisas A, B,...N y, por tanto, de su producto, podemos obtener la conclusión Y con valor de verdad V, siempre y cuando dicho esquema de inferencia sea una ley lógica, es decir su tabla de verdad nos muestre que es una tautología.
Por la regla de separación podremos concluir Y, de forma independiente como verdad.
Dada la poca operatividad de las tablas de verdad, el cálculo se construye como una cadena deductiva aplicando a las premisas o a los teoremas deducidos las leyes lógicas utilizadas como reglas de transformación, como se expone en cálculo lógico.
Concepto de modelo
Cuando en un Cálculo C, se establece una "correspondencia" de cada símbolo con elementos determinados individuales distinguibles entre sí, de un Universo L, real, (tal universo L no es un conjunto vacío, por las mismas condiciones que hemos establecido) ENTONCES se dice que L es un MODELO de C.
El lenguaje natural como modelo de un cálculo lógico
Naturalmente el cálculo lógico es útil porque puede tener aplicaciones, pero ¿en qué consisten o cómo se hacen tales aplicaciones?
Podemos considerar que el lenguaje natural es un modelo de C si podemos someterlo, es decir, aplicarle una correspondencia en C.
Para ello es necesario someter al lenguaje natural a un proceso de formalización de tal forma que podamos reducir las expresiones lingüísticas del lenguaje natural a EBFs de un cálculo mediante reglas estrictas manteniendo el sentido de verdad lógica de dichas expresiones del lenguaje natural. Esto es lo que se expone en cálculo lógico.
Las diversas formas en que tratemos las expresiones lingüísticas dan lugar a sistemas diversos de formalización y cálculo:
- Cálculo proposicional o cálculo de enunciados
- Cuando se toma la oración simple significativa del lenguaje natural con posible valor de verdad o falsedad como una proposición atómica, como un todo sin analizar.
La oración simple: "Llueve", o "Las farolas se apagan por la noche" son consideradas como posible valor de verdad o falsedad de una variable "p".
- Cálculo como lógica de clases
- Cuando se toma la oración simple significativa del lenguaje natural con posible valor de verdad o falsedad como resultado del análisis de la oración como una relación de individuos o posibles individuos que pertenecen o no pertenecen a una clase.
- Siendo una clase el criterio, como una propiedad o una definición, que permite ordenar a todos los posibles individuos de un Universo determinado como pertenecientes o no pertenecientes a dicha clase. La clase como propiedad o definición define al conjunto de posibles individuos, pero es independiente de la existencia de dichos individuos; no se identifica con el conjunto de individuos. Clase = Pegaso; Propiedad o definición = Caballo con alas; Individuos = ninguno.
- Esta es la forma en la que en la actualidad se interpreta la lógica silogística de Aristóteles, que queda así se reducida a un cálculo según la lógica de clases.
La oración simple "Todos los caballos corren por el campo" está analizada como: La clase de todos los posibles seres que corren por el campo (B) incluye a la clase formada por todos los posibles seres que sean caballos (A).
- Cálculo de predicados o cuantificacional
- Cuando se toma la oración simple significativa del lenguaje natural con posible valor de verdad o falsedad como resultado del análisis de la misma de forma que una posible función predicativa (P), se predica de unos posibles sujetos variables (x) [tomados en toda su posible extensión: (Todos los x); o referente a algunos indeterminados: (algunos x)], o de una constante individual existente (a).
La oración simple "los perros muerden" se formaliza de la siguiente manera:
 Todos los posibles perros;
Todos los posibles perros;P = todas las posibles acciones de morder.
 Para todo x (siendo x un perro) x muerde = Todos los perros muerden.
Para todo x (siendo x un perro) x muerde = Todos los perros muerden.En el caso de Desko que es mi perro al que simbolizo como una constante a:
P(a) = Mi perro Desko muerde.
- Cálculo como lógica de relaciones
- Cuando se toma la oración simple significativa con posible valor de verdad propio, verdado o falso, como resultado del análisis de la oración como una relación "R" que se establece entre un sujeto y un predicado.
Así la oración simple "Antonio es mayor que Pedro", se considera y simboliza bajo la relación "ser mayor que" (R) que se da entre Antonio (a) y Pedro (p) y se simboliza como aRp.
La simbolización y formación de EBFs en cada uno de esos cálculos, así como las reglas de cálculo se trata en cálculo lógico.





No hay comentarios:
Publicar un comentario